Teckel — An Interpreter for Abstract Algorithms in LaTeX

by Dick Grune

**** Provisional ****

Contents

• Short Intro
• The Program Execution Model
• Project Status
• Further Documentation

Short Intro

Teckel is an interpreter for non-deterministic and deterministic algorithms written in a mathematical style and expressed in LaTeX. For example, the Teckel program

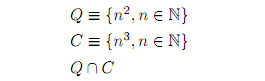
resulting from the LaTeX code

%Teckel on
\Tdefine{Q}{\{ n ^ 2 , n \in \mathbb{N} \}}
\Tdefine{C}{\{ n ^ 3 , n \in \mathbb{N} \}}
\Toutput{Q \cap C}
%Teckel off

And the Teckel program segment

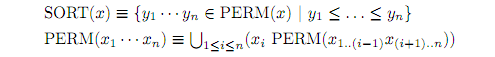
resulting from

%Teckel on
\begin{quote}
\Tdefine{\mathrm{SORT}(x)}{
	\{ y_1 \cdots y_n \in \mathrm{PERM}(x) ~ | ~
	y_1 \leq \ldots \leq y_n \}
}
\Tdefine{\mathrm{PERM}(x_1 \cdots x_n)}{
	\bigcup_{1 \leq i \leq n}
	( x_i ~ \mathrm{PERM} (x_{1 ..(i-1)} x_{(i+1)..n}))
}
\end{quote}
%Teckel off

Teckel tries hard to find solutions, avoid getting sidetracked by infinite dead ends, and produce at least some results in finite time. On the other hand, speed has consistently been sacrificed for power.

Teckel allows the same LaTeX text to be run and published, thus cutting out one conversion layer and a lot of programming. It is also a convenient means for running non-deterministic programs.

The Program Execution Model

The program is stored as a binary tree; complex operations have been "binarized". The tree is reduced (in the functional-programming sense of the word) by the "Teckel", who searches the tree, finds a redex, reduces it, and repeats the process. To prevent the Teckel from getting stuck in (infinite) dead ends, the search for the redex is performed in breadth-first fashion. Note that even AND nodes need to be reduced breadth-first: one of the branches may loop forever while another one comes up with the answer False. If the tree or a subtree reduces to a value, breadth-first search will find it in finite time.

The Teckel finds the redex as follows. It starts at the top of the tree. If the node has one unreduced child, it goes to that child. If the node has two unreduced children, and if it went to the left child last time the node was visited, it now goes to the right child, and vice versa. It repeats this procedure at the node thus reached, etc. Eventually the Teckel finds a node without unreduced children. This is the redex; the Teckel performs the action the node requires and starts from the top again. This procedure distributes the available processing power fairly over the tree, and guarantees that every node will come up for reduction in finite time.

Project Status

Some parts work:

but nothing Internet-worthy yet. See the documentation. The time scale of this project is several/many years.

Documentation

This is all very much under construction.

• Teckel Manual
• Unix-like Teckel manpage
• The context-free syntax of Teckel

• Teckel design considerations
• Lexical analyzer design considerations
• Prescan design considerations
• Syntax design considerations
• Postscan design considerations
• Interpreter design considerations
• Code design considerations

Further documents

• A full cyclic reference-counting garbage collector (no longer in use since it proved unnecessary)

Last update: Nov. 3, 2014
Updates will be released as they become available.

---

[Home Page]

---

... and my name is not Richard ...